Voor deze proef is het verband gebruikt. Voor de bepaling van de (constante) acceleratie door de tijd te meten over een afstand is de vergelijking gebruikt wat herschreven is naar . Voor het bepalen van de acceleratie wordt gebruik gemaakt van de bewegings vergelijkingen en wat gesubtitueert stelt dat wat neerkomt op en versimpeld kan worden naar
Uitvoering 1: CDC aanpak¶
Elke groepje bepaalt nauwkeurig de versnelling bij een enkele massa . De metingen worden gecombineerd door de docent: . Gezamenlijk wordt het resultaat besproken, de voorspelde grafiek is op het bord weergegeven m.b.v. geogebra. De metingen worden door de leerlingen toegevoegd.
Per enkele massa kan over verschillende afstanden van de tijd van aankomt worden gemeten. Neem als voorbeeld de volgende tabellen;
!Hier komen de tabellen te staan met verschillende klik dingen.!
Uit deze tabellen vallen de volgende grafieken te plotten.
| (g) | (m/s) | (m/s) |
|---|---|---|
| 3 | 0.13 | |
| 6 | 0.27 | |
| 9 | 0.42 | |
| 12 | 0.978 | 0.54 |
| 15 | 1.109 | 0.66 |
| 18 | 1.205 | 0.78 |
| 21 | 1.284 | 0.90 |
| 24 | 1.360 | 1.01 |
| 27 | 1.407 | 1.12 |
| 30 | 1.479 | 1.24 |

uit de fit is: 0.2078 ± 0.0006 kg.
gewogen is .1993176±0.00005 kg.
Hier met de stopwatch
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
from scipy.optimize import curve_fit
# Constante zwaartekracht
g = 9.81 # m/s²
# Afstand in meter
s = np.array([0.101, 0.151, 0.201, 0.251, 0.301, 0.351, 0.401, 0.451,
0.501, 0.551, 0.601, 0.651, 0.701, 0.751, 0.801, 0.851])
# Tijdgegevens per massa
t_data = {
12: [0.63859, 0.78181, 0.90827, 1.0062, 1.1023, 1.1657, 1.2498, 1.3122,
1.385, 1.4543, 1.5252, 1.6044, 1.662, 1.713, 1.7759, 1.8347],
16: [0.56258, 0.67357, 0.77359, 0.87289, 0.96362, 1.029, 1.1039, 1.1663,
1.2265, 1.2908, 1.3441, 1.401, 1.4522, 1.5035, 1.5479, 1.6006],
20: [0.50587, 0.6126, 0.69814, 0.79216, 0.86503, 0.93244, 0.98425, 1.0492,
1.1088, 1.1627, 1.2136, 1.2648, 1.3187, 1.3528, 1.4012, 1.4428],
24: [0.47255, 0.56921, 0.65457, 0.72807, 0.79512, 0.85813, 0.91682, 0.97142,
1.02200, 1.07200, 1.11790, 1.16050, 1.20710, 1.24430, 1.28890, 1.32730],
28: [0.42545, 0.52677, 0.60986, 0.6827, 0.74445, 0.8014, 0.85306, 0.90861,
0.95552, 0.99331, 1.0457, 1.0883, 1.1273, 1.1689, 1.2076, 1.2422],
32: [0.40777, 0.49888, 0.57568, 0.6398, 0.69925, 0.75268, 0.80561, 0.85611,
0.89989, 0.94311, 0.98493, 1.0244, 1.0604, 1.0988, 1.1344, 1.1703],
}
# Model
def s_model(t, a):
return 0.5 * a * t**2
# Formatter
def komma_formatter(x, pos):
return f"{x:.4f}".replace('.', ',')
def komma_formatter_y(y, pos):
return f"{y:.3f}".replace('.', ',')
# Plot en fitresultaten
plt.figure(figsize=(10, 6))
colors = plt.cm.viridis(np.linspace(0, 1, len(t_data)))
fit_resultaten = {}
for (mass, t_vals), color in zip(t_data.items(), colors):
t_vals = np.array(t_vals)
popt, pcov = curve_fit(s_model, t_vals, s)
a_fit = popt[0]
a_std = np.sqrt(np.diag(pcov))[0]
fit_resultaten[mass] = (a_fit, a_std)
# Plot punten en fit
plt.plot(t_vals, s, 'o', color=color, label=f'{mass} g')
t_fit = np.linspace(0.95 * min(t_vals), 1.05 * max(t_vals), 300)
s_fit = s_model(t_fit, a_fit)
plt.plot(t_fit, s_fit, '-', color=color)
# Labels en layout
plt.xlabel('$t$ (s)')
plt.ylabel('$s$ (m)')
plt.legend(title='Massa $m_2$')
plt.grid(True)
plt.gca().xaxis.set_major_formatter(FuncFormatter(komma_formatter))
plt.gca().yaxis.set_major_formatter(FuncFormatter(komma_formatter_y))
plt.tight_layout()
plt.show()
# Print fitresultaten als tabel
print("Versnelling per massa m_2:")
for mass, (a, da) in fit_resultaten.items():
print(f"m_2 = {mass:2d} g → a = {a:.4f} ± {da:.4f} m/s²")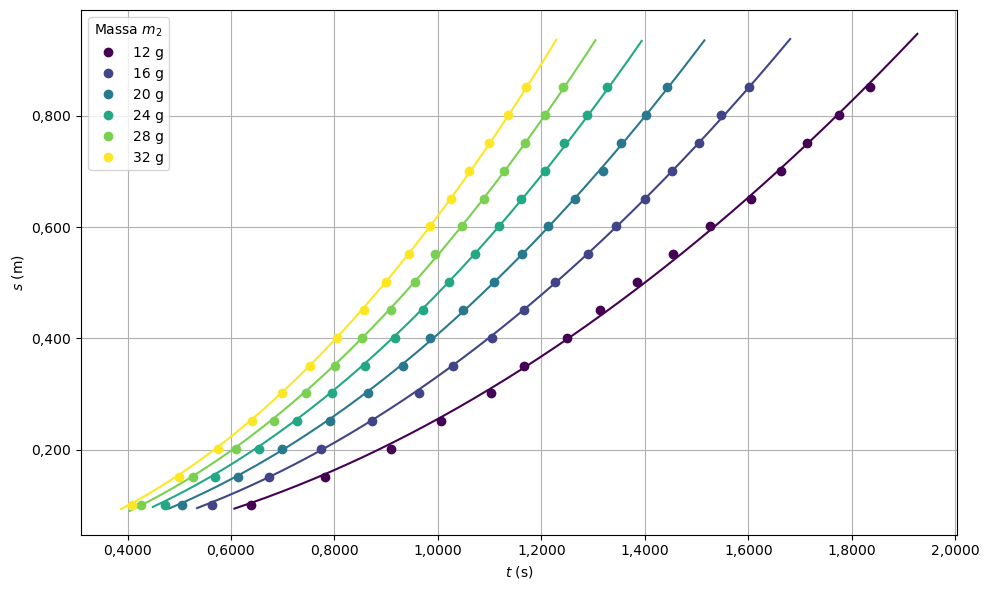
Versnelling per massa m_2:
m_2 = 12 g → a = 0.5105 ± 0.0018 m/s²
m_2 = 16 g → a = 0.6642 ± 0.0009 m/s²
m_2 = 20 g → a = 0.8152 ± 0.0014 m/s²
m_2 = 24 g → a = 0.9623 ± 0.0017 m/s²
m_2 = 28 g → a = 1.1001 ± 0.0017 m/s²
m_2 = 32 g → a = 1.2407 ± 0.0015 m/s²
De verkregen coeficienten kunnen gebruikt worden voor het opstellen van het diagram wat er als volgt uit ziet;
Source
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from matplotlib.ticker import FuncFormatter
# Formatterfunctie voor komma's
def komma_formatter(x, pos):
return format(x, '.4f').replace('.', ',')
def komma_formatter_y(x, pos):
return format(x, '.3f').replace('.', ',')
# Constante zwaartekracht
g = 9.81 # m/s²
# Gegevens
m2 = np.array([12, 16, 20, 24, 28, 32])
a = np.array([0.5105, 0.6642, 0.8152, 0.9623, 1.1001, 1.2420])
# Onzekerheden in a (indien beschikbaar)
a_err = np.array([0.0018, 0.0009, 0.0014, 0.0017, 0.0017, 0.0021])
m2_err = np.zeros_like(a_err) # Geen onzekerheid in massa
# Atwoodmodel met vaste g
def atwood_model(m2, m1):
return (g * m2) / (m1 + m2)
# Curve fit met alleen m1 als parameter
params, cov = curve_fit(atwood_model, m2, a, sigma=a_err, absolute_sigma=True, p0=[200])
m1_fit = params[0]
m1_err = np.sqrt(np.diag(cov))[0]
# Print resultaten
print(f"Geschatte massa karretje m₁ = ({m1_fit:.2f} ± {m1_err:.2f}) g")
# Plotten
m2_plot = np.linspace(0.95 * min(m2), 1.05 * max(m2), 300)
a_fit = atwood_model(m2_plot, *params)
plt.figure(figsize=(10, 6))
plt.scatter(m2, a, label='Meetpunten', color='black')
plt.plot(m2_plot, a_fit, label='Fit: $a = \\frac{{g \\cdot m_2}}{{m_1 + m_2}}$', color='green')
plt.xlabel('$m_2$ [g]')
plt.ylabel('$a$ [m/s²]')
plt.grid(True)
plt.legend()
plt.gca().xaxis.set_major_formatter(FuncFormatter(komma_formatter))
plt.gca().yaxis.set_major_formatter(FuncFormatter(komma_formatter_y))
plt.tight_layout()
plt.show()Geschatte massa karretje m₁ = (220.70 ± 0.17) g
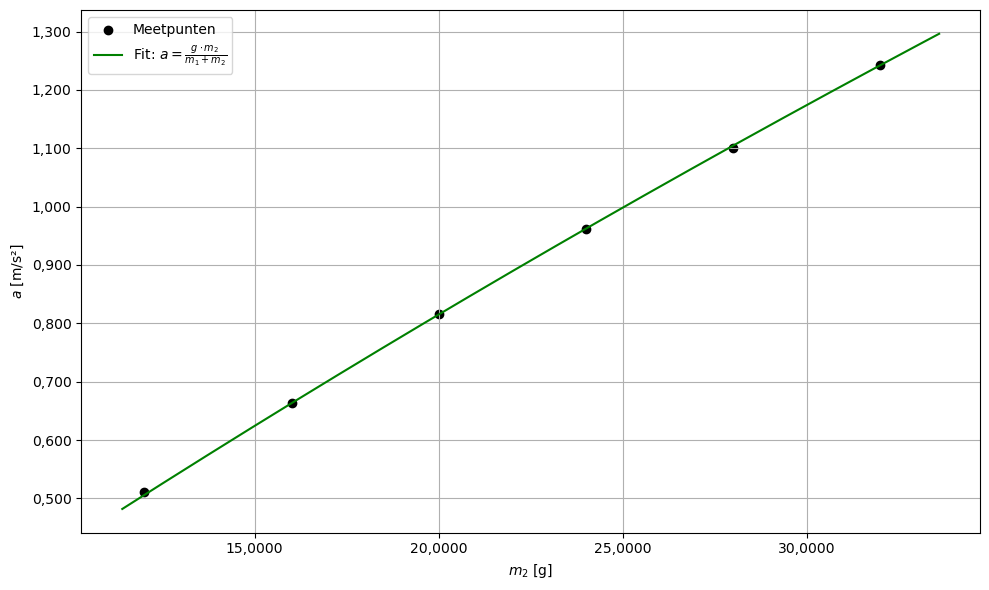
De massa van het wagentje letterlijk gewogen bedraagt terwijl de experiment bepaalde massa is.
Uitvoering 2¶
Elk groepje bepaalt op basis van een éénpuntsmeting (welke afstand kun je het beste gebruiken en waarom?) de versnelling. Ze variëren zelf de massa van (). Welke massa’s gebruik je en waarom?
Met behulp van de stopwatch wordt de volgende data verkregen:
**Tabel**Met behulp van de speedgate wordt de volgende data verkregen:
**tabel**Deze data wordt gepresenteerd in de volgende grafiek;
Source
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from matplotlib.ticker import FuncFormatter
import locale
# Nederlandse notatie instellen (komma als decimaalteken)
try:
locale.setlocale(locale.LC_NUMERIC, 'nl_NL.UTF-8')
except:
pass # Sla fout over als locale niet beschikbaar is
# Formatterfuncties
def komma_formatter(x, pos):
return format(x, '.4f').replace('.', ',')
def komma_formatter_y(x, pos):
return format(x, '.3f').replace('.', ',')
# Gegevens
m2 = np.array([
3.0143, 4.0116, 5.0202, 6.0195, 7.0173, 8.0152, 9.0132,
10.0120, 11.0303, 12.0292, 12.9503, 13.9493, 14.9469, 15.9551, 16.9529,
17.9732, 18.9799, 19.9797, 20.9762, 21.9847, 22.9818, 23.9800, 24.9779,
25.9860, 27.0051, 28.0043, 29.0310, 30.0019])
a = np.array([
0.134, 0.170, 0.209, 0.266, 0.326, 0.369, 0.421,
0.455, 0.499, 0.543, 0.5824, 0.6198, 0.6595, 0.6980, 0.7363,
0.7769, 0.8241, 0.8614, 0.8996, 0.9357, 0.9769, 1.012, 1.050,
1.087, 1.124, 1.161, 1.198, 1.242])
# g als constante
g_const = 9.81
# Model met vaste g
def atwood_model_fixed_g(m2, m1):
return (g_const * m2) / (m2 + m1)
# Curve fit met alleen m1 als parameter
params, cov = curve_fit(atwood_model_fixed_g, m2, a, p0=[200])
m1_fit = params[0]
m1_err = np.sqrt(np.diag(cov))[0]
# Fitresultaat
print(f"Gebruik vaste g = 9,81 m/s²")
print(f"Geschatte m₁ (karretje) = ({m1_fit:.2f} ± {m1_err:.2f}) g")
# Fitwaarden voor plot
m2_plot = np.linspace(min(m2), max(m2), 300)
a_model = atwood_model_fixed_g(m2_plot, m1_fit)
# Grenzen instellen (0.95 * min tot 1.05 * max)
x_min, x_max = 0.95 * min(m2), 1.05 * max(m2)
y_min, y_max = 0.95 * min(a), 1.05 * max(a)
# Plot
fig, ax = plt.subplots(figsize=(10, 6))
ax.scatter(m2, a, label='Meetpunten', color='black')
ax.plot(m2_plot, a_model, label='Fit: $a = \\frac{g \\cdot m_2}{m_1 + m_2}$', color='green')
ax.set_xlabel('$m_2$ [g]')
ax.set_ylabel('$a$ [m/s²]')
ax.set_xlim([x_min, x_max])
ax.set_ylim([y_min, y_max])
ax.grid(True)
ax.legend()
# Formatter met komma's
ax.xaxis.set_major_formatter(FuncFormatter(komma_formatter))
ax.yaxis.set_major_formatter(FuncFormatter(komma_formatter_y))
plt.tight_layout()
plt.show()Gebruik vaste g = 9,81 m/s²
Geschatte m₁ (karretje) = (207.99 ± 0.40) g
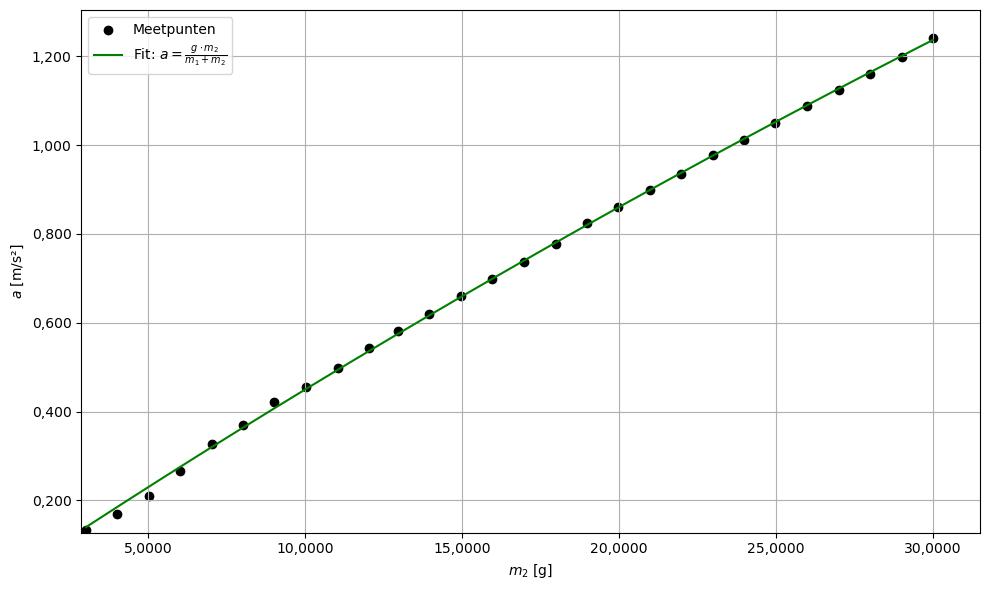
De gewoggen massa van de kar bedreaagt terwijl het experiment heeft bepaald dat .
Bijlage A – Gewichten¶
| Welke | Drager (g) | Zwart klein (g) | Zwart middel (g) | Zilver klein (g) | Zilver middel (g) |
|---|---|---|---|---|---|
| gem | 2,0 | 1,0 | 2,0 | 5,0 | 10,0 |
| 1 | 1,9953 | 0,9974 | 1,9984 | 5,0210 | 9,9381 |
| 2 | 2,0154 | 0,9989 | 1,9959 | 10,0308 | |
| 3 | 1,9940 | 2,0058 |
Bijlage B – Tabel met gegevens¶
Versnelling uit valafstand:¶
Berekening:
Formule:
| m₂ [g] | t [s] | aₜ [m/s²] |
|---|---|---|
| 3,0143 | 3,64 | 0,134 |
| 4,0116 | 3,23 | 0,170 |
| 5,0202 | 2,91 | 0,209 |
| 6,0195 | 2,58 | 0,266 |
| 7,0173 | 2,33 | 0,326 |
| 8,0152 | 2,19 | 0,369 |
| 9,0132 | 2,05 | 0,421 |
Versnelling uit eindsnelheid:¶
Berekening:s_v = 99,6 cm - 11,5 cm = 0,881 m
Formule: v² = 2as → a = v² / 2s
| m₂ [g] | t [s] | aₜ [m/s²] |
|---|---|---|
| 10,0120 | 0,895 | 0,455 |
| 11,0303 | 0,938 | 0,499 |
| 12,0292 | 0,978 | 0,543 |
| 12,9503 | 1,013 | 0,5824 |
| 13,9493 | 1,045 | 0,6198 |
| 14,9469 | 1,078 | 0,6595 |
| 15,9551 | 1,109 | 0,6980 |
| 16,9529 | 1,139 | 0,7363 |
| 17,9732 | 1,170 | 0,7769 |
| 18,9799 | 1,205 | 0,8241 |
| 19,9797 | 1,232 | 0,8614 |
| 20,9762 | 1,259 | 0,8996 |
| 21,9847 | 1,284 | 0,9357 |
| 22,9818 | 1,312 | 0,9769 |
| 23,9800 | 1,335 | 1,012 |
| 24,9779 | 1,360 | 1,050 |
| 25,9860 | 1,384 | 1,087 |
| 27,0051 | 1,407 | 1,124 |
| 28,0043 | 1,430 | 1,161 |
| 29,0310 | 1,453 | 1,198 |
| 30,0019 | 1,479 | 1,242 |